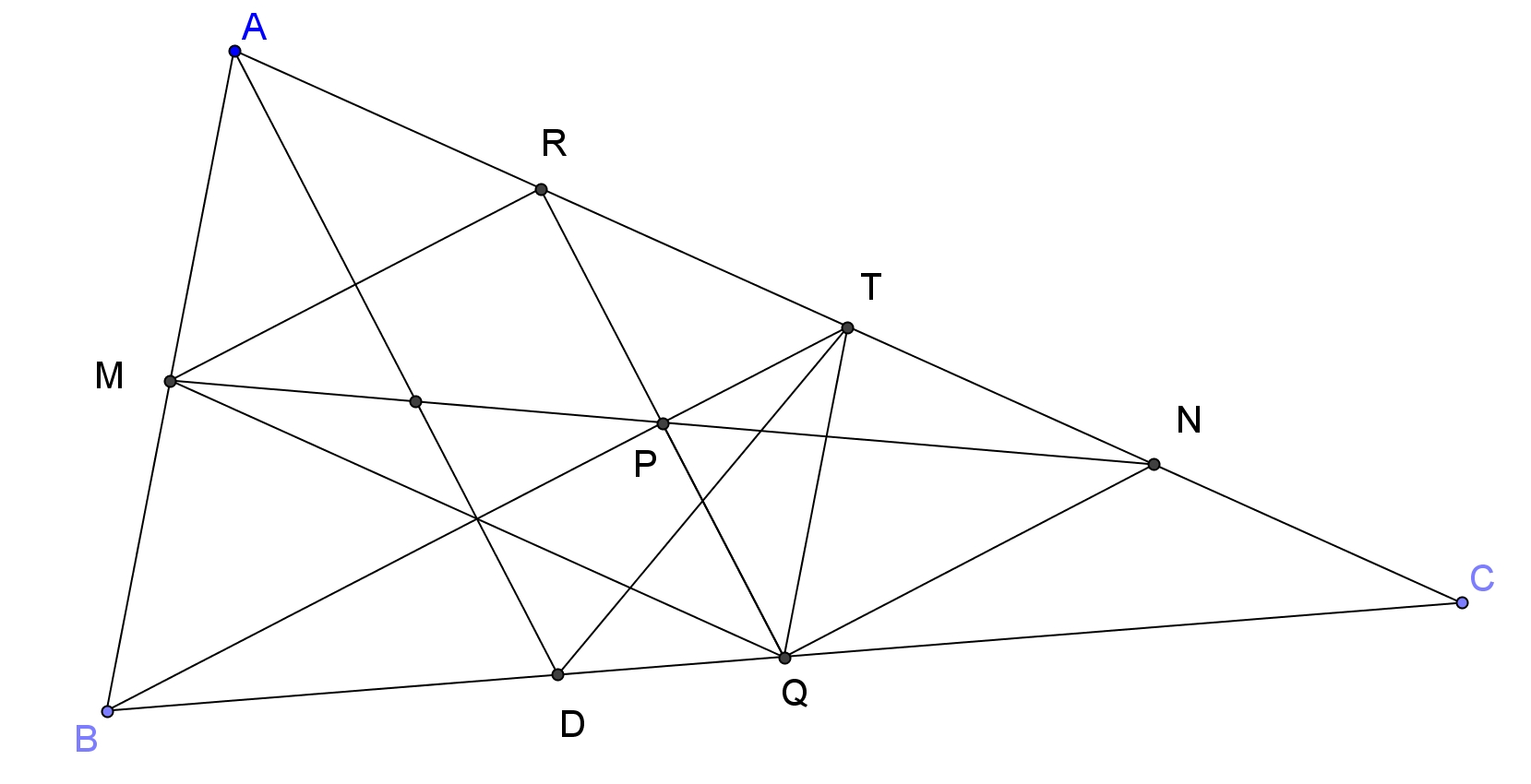
Legyenek R, T, N negyedelő pontok, ezért RN az AC fele.
MQ az ABC háromszög középvonala, ezért MQ||AC, és MQ az AC fele.
Tehát MQNR paralelogramma (szemközti oldalai párhuzamosak és egyenlők).
A paralelogramma átlói felezik egymást, tehát az RQ felezőpontja az MN felezőpontja is.
Mivel AD szögfelező
\frac{AB}{AC}=\frac{BD}{DC}=\frac12

Ha QC= x jelölést bevezetjük, akkor
BD=\frac{2x}{3};\, DQ=x-\frac{2x}{3}=\frac{x}{3};\, CD=x+\frac{x}{3}=\frac{4x}{3}
Tehát:
\frac{CA}{CR}=\frac{CD}{CQ}=\frac43
Tehát a párhuzamos szelők tétele alaján AD||RQ.
A CAD és CRQ háromszögek hasonlók:
\frac{CA}{CR}=\frac{CD}{CQ}=\frac{AD}{RQ}=\frac43
Mivel RQ=2PQ
\frac{AD}{RQ}=\frac{AD}{2PQ}=\frac43
\frac{AD}{PQ}=\frac83