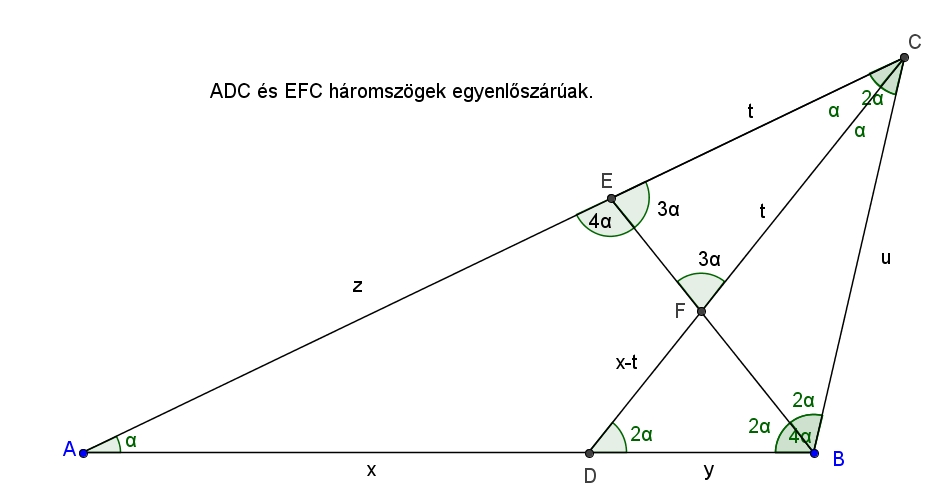
A fenti jelölésekkel a következőt kell igazolnunk: 

	\frac{1}{x+y}+\frac{1}{z+t}=\frac 1u
Beszorozva a közös nevezőkkel a következő állítást kell igazolnunk. 
	zu+tu+xu+yu=xz+xt+yz+yt
A CD szögfelezőre felírjuk a szögfelezőtételt: 
	\frac{z+t}{x}=\frac{u}{y}
Kifejtve: 
	xu=zy+ty\,\,(1)
A BE szögfelezőre felírjuk a szögfelezőtételt: 
	\frac{x+y}{z}=\frac{u}{t}
Kifejtve: 
	zu=xt+yt\,\,(2)
A BF szögfelezőre felírjuk a szögfelezőtételt: 
	\frac{y}{x-t}=\frac{u}{t}
Kifejtve: 
	yt+ty=xu\,\,(3)
Az AEB és CDB háromszögek hasonlóságából: 
	\frac{z}{u}=\frac{x+y}{x}
Kifejtve: 
	xu+yu=xz\,\,(4)
A négy egyenletet összeadjuk, egy-egy xu és yt kiesik, és pontosan a keresett egyenlőség marad.